• wisha@lemmy.mlEnglish
      10911·
      5 months ago

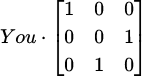
      I just downvoted your comment.

      FAQ

      What does this mean?

      The amount of points on your comment will be decreased by one. The deduction will be federated across thousands of Lemmy instances, bringing you shame from across the Fediverse.

      Why did you do this?

      There are several reasons I may deem a comment to be unworthy of positive or neutral points. These include, but are not limited to:

      • Rudeness towards other users,
      • Spreading incorrect information,
      • Sarcasm not correctly flagged with a /s.

      As this is your first time receiving my downvote, I will provide reasons (listed below) to help you avoid making these mistakes again. Note that this will not be the case with future downvotes.

      • Writing variables next to each other to form words. “Y o u” is not an English word. If you want the English word “You” in LaTeX math mode, write \text{You}.
      • Your “rotation matrix” has determinant of -1, meaning it is not a rotation matrix. Propaganda promoting improper rotations will not be tolerated on mander.xyz.

      Am I banned from the Lemmy?

      No - not yet. But you should refrain from making comments like this in the future. Otherwise I will be forced to issue an additional downvote, which may put your commenting and posting privileges in jeopardy.

      I don’t believe my comment deserved a downvote. Can you un-downvote it?

      Sure, mistakes happen. But only in exceedingly rare circumstances will I undo a downvote. If you would like to issue an appeal, shoot me a private message explaining what I got wrong. I tend to respond to PMs within several minutes. Do note, however, that over 99.9% of downvote appeals are rejected, and yours is likely no exception.

      How can I prevent this from happening in the future?

      Accept the downvote and move on. But learn from this mistake: your behavior will not be tolerated on mander.xyz or the Fediverse as a whole. I will continue to issue downvotes until you improve your conduct. Remember: Posting is privilege, not a right.

      • wisha@lemmy.mlEnglish
        621·
        5 months ago

        I didn’t actually downvoted your comment but apprently someone did and now I look like an asshole 😢.

        • skulblaka@startrek.websiteEnglish
          391·
          5 months ago

          Honestly with a writeup like this I wouldn’t be mad about it even if you did, this is excellent. I wish all my downvoted comments got this kind of attention.

          • wisha@lemmy.mlEnglish
            282·
            5 months ago

            It’s an old copypasta from reddit haha. I modified it to add the Fediverse stuff and my complaints with LaTex and improper rotation.

  • rescue_toaster@lemm.eeEnglish
    29·
    5 months ago

    As someone that grades undergraduates, I’m happy that they not use the letter “x” to imply multiplication.

    • credo@lemmy.worldEnglish
      7·
      5 months ago

      I don’t understand why we teach that to children, just to turn around and tell them not to do it a few years later.

      • davidgro@lemmy.worldEnglish
        81·
        5 months ago

        I suppose kids aren’t great at centering a dot. But they could draw a six pointed * as easily as an x, it’s one more line.

  • AeonFelis@lemmy.worldEnglish
    15·
    5 months ago

    \cdot master race. \times users should just use Microsoft Word (unless it’s for a Cartesian product or for cross product, of course)

  • the_beber@lemm.eeEnglish
    11·
    5 months ago

    \cdot for matrix multiplication and the dot product, \times for cross product and nothing (or *, if I want to write it explicitly and have no convolution in the expression) for regular multiplication.

  • ofcourse@lemmy.mlEnglish
    8·
    5 months ago
    • \cdot for vectors and in some cases, scalar variables, e.g., x \cdot y
    • \times for numbers, e.g., 2 \times 8
    • nothing for combination and scalars, e.g., 2x or xy